Mohsen Sadr

Mohsen Sadr

About Me

I am an applied mathematician working at the intersection of computational physics, statistical modeling, and machine learning. I am passionate about bringing AI-based solutions from physics-aware agents to data-driven surrogate models into the fusion energy and space travel industries, with the goal of dramatically accelerating engineering design cycles.

Currently, I am a Founder Fellow at the Paul Scherrer Institute (PSI) and a Research Affiliate at MIT. At PSI (2023–2025), I worked on optimal transport and collaborated with Dr. Andreas Adelmann on scaling OPALX—a particle accelerator simulation library—for exascale HPC platforms. At MIT (2021–2023), I worked with Prof. Nicolas Hadjiconstantinou on general-purpose variance-reduced Monte Carlo methods for kinetic equations. Prior to that, I was a postdoc with Prof. Laurent Villard at the Swiss Plasma Center (EPFL), contributing to ORB5, a gyrokinetic particle-in-cell code for confined plasma simulations. I received my PhD in Applied Mathematics from RWTH Aachen University, advised by Prof. Manuel Torrilhon and Prof. Hossein Gorji, where my dissertation focused on efficient Monte Carlo methods for dense gas, liquid, and phase-transition kinetics.

News

Feb 2026

PSI Founder Fellowship for Physics-based AI Platform

Awarded a PSI Founder Fellowship (up to 150,000 CHF) to develop an AI-based platform that accelerates and reduces the cost of physical simulations for fusion energy, aerospace, and semiconductor technologies. The fellowship includes coaching and advisory services from PSI's technology transfer team and external experts.

PSI Media Release Swiss Federal Government
Feb 2026

New preprint: VR-PIC for Vlasov–Poisson equations

Our paper “VR-PIC: An entropic variance-reduction method for particle-in-cell solutions of the Vlasov–Poisson equation” is now on arXiv. We extend the entropic variance reduction framework to the PIC method, achieving 1–4 orders of magnitude computational speedup in the low-signal regime while maintaining high accuracy.

arXiv Code
Oct 2025

Paper accepted in Transactions on Machine Learning Research (TMLR)

Our paper “Data-Driven Discovery of PDEs via the Adjoint Method” has been accepted in TMLR. We present an adjoint-based method for discovering governing PDEs from data, formulated as a PDE-constrained optimization problem with analytically derived gradients.

OpenReview Code

Projects

Non-equilibrium Multiphase Flows

In this line of research, I designed a stochastic process for modeling short and long-range interactions of monatomic particles that follows the exact kinetic equation up to desired moments with a feasible computational complexity that scales linearly with the number of particles. For details on the developed method, see [7, 8, 9]. These methods have been implemented in a particle-in-cell code called PICLas. As a showcase, here a simulation of Argon's density experiencing the spinodal decomposition is presented.

Excitation of Confined Plasma

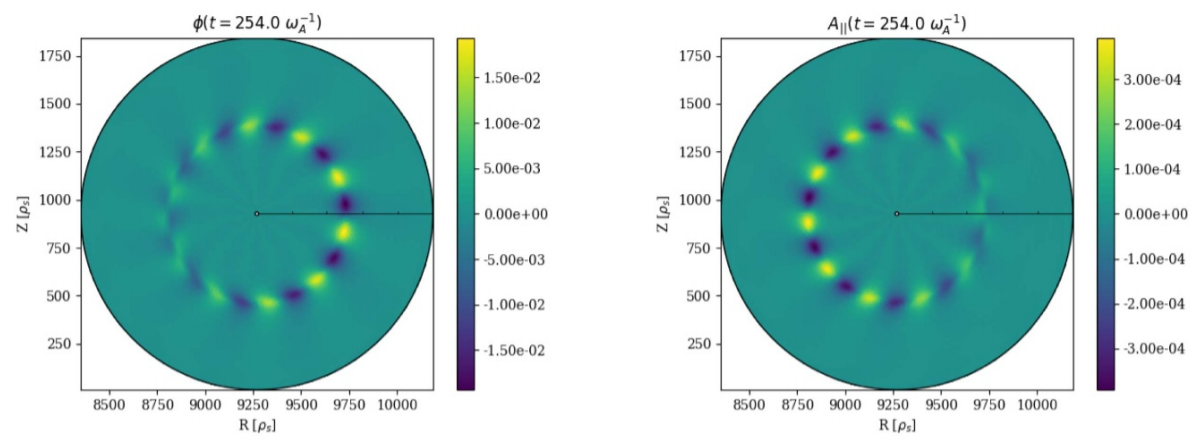
Stabilizing a confined plasma in a fusion device is one of the main challenges in designing such a system. Often, it is worthwhile to study the growth/dissipation rates of modes of the system to better control the plasma. I have worked on excitation of Alfven modes in a confined plasma using a well-established particle-in-cell and gyrokinetic code called ORB5. As a showcase, electrostatic and magnetic potential fields are shown here where the mode of interest is successfully excited using a so-called antenna. For more details, see [15].

Visualization of excited Alfven modes

Variance Reduction Method

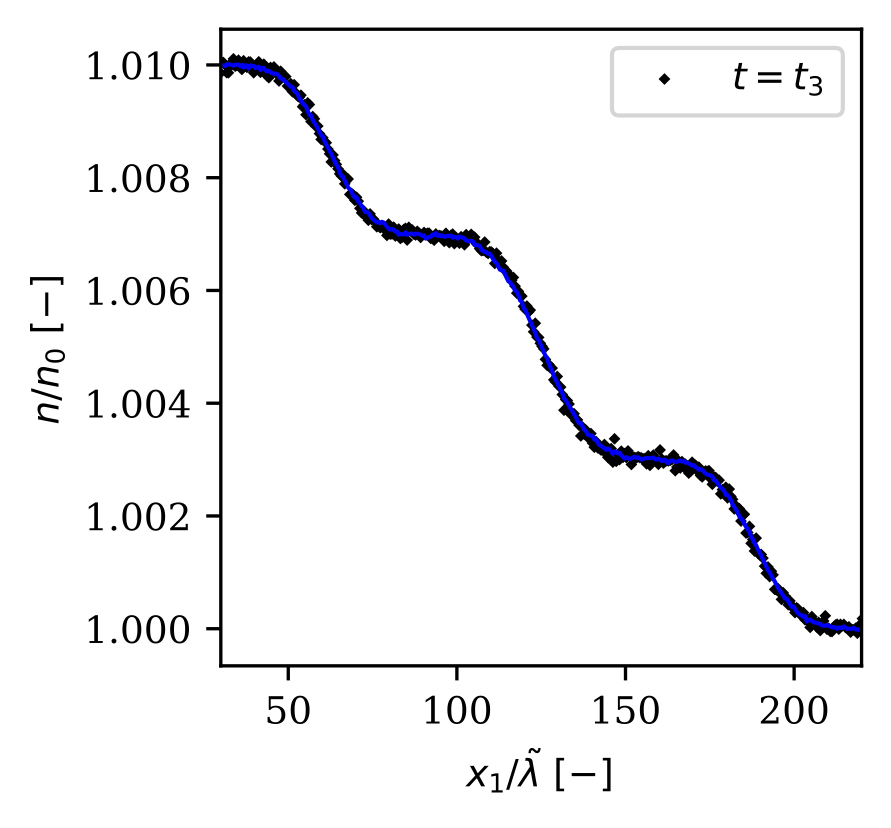
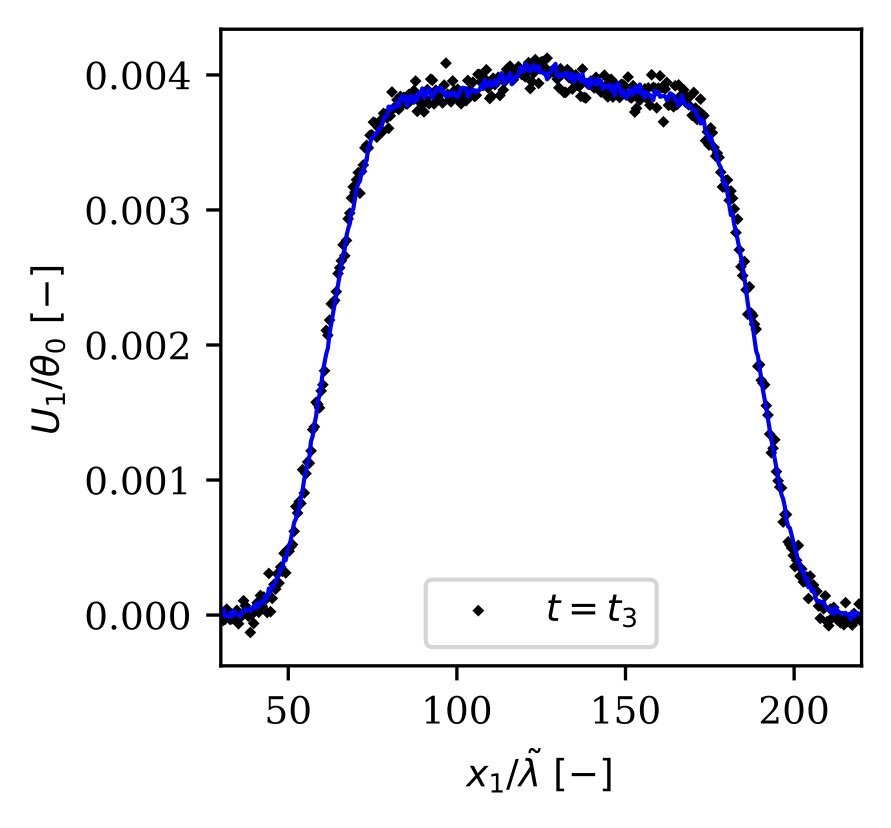
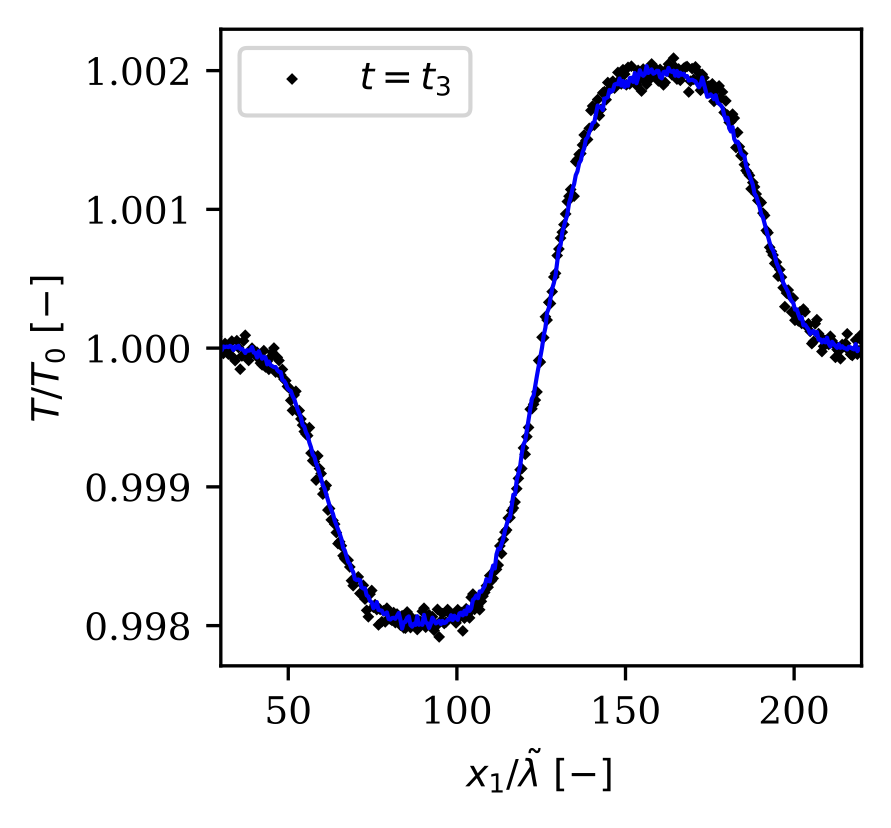
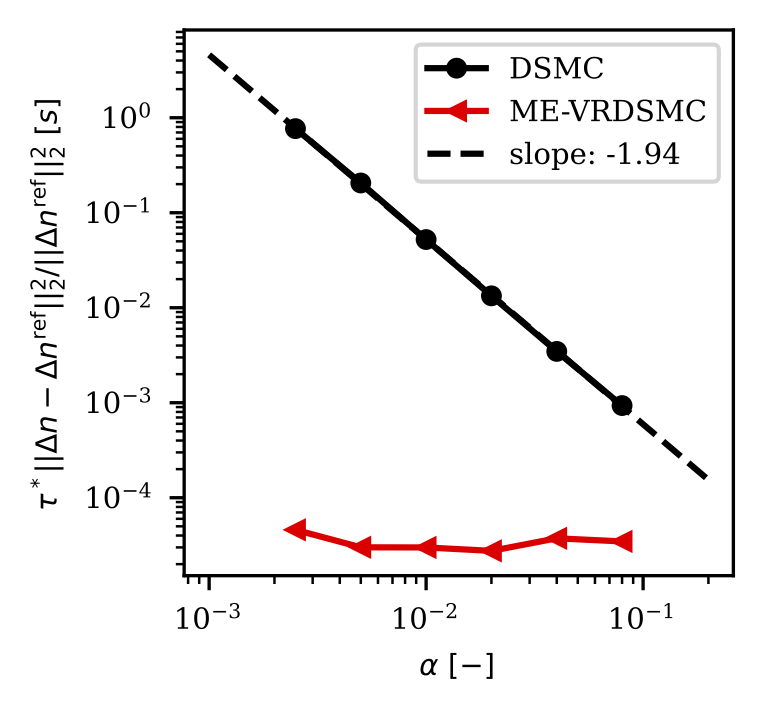
One of the main challenges in interpreting the solution of statistical models is noise. I have developed a general-purpose and entropy-based variance reduction method for stochastic processes where the target density is around an equilibrium/control-variate density. In this project, I devised a consistent and least-biased evolution equation for the importance weights of the Boltzmann and Fokker-Planck equation. The following figures show the snapshot estimate of number density, bulk velocity, and temperature for the Sod-Shock tube test case. We also show how the noise varies with respect to the signal for the standard Monte Carlo and the introduced variance reduction method. For details, see [4], [5] and [6].

Number density for Sod-Shock tube test case Bulk velocity for Sod-Shock tube test case Temperature for Sod-Shock tube test case Noise variation vs signal for variance reduction

Optimal Transport Problem

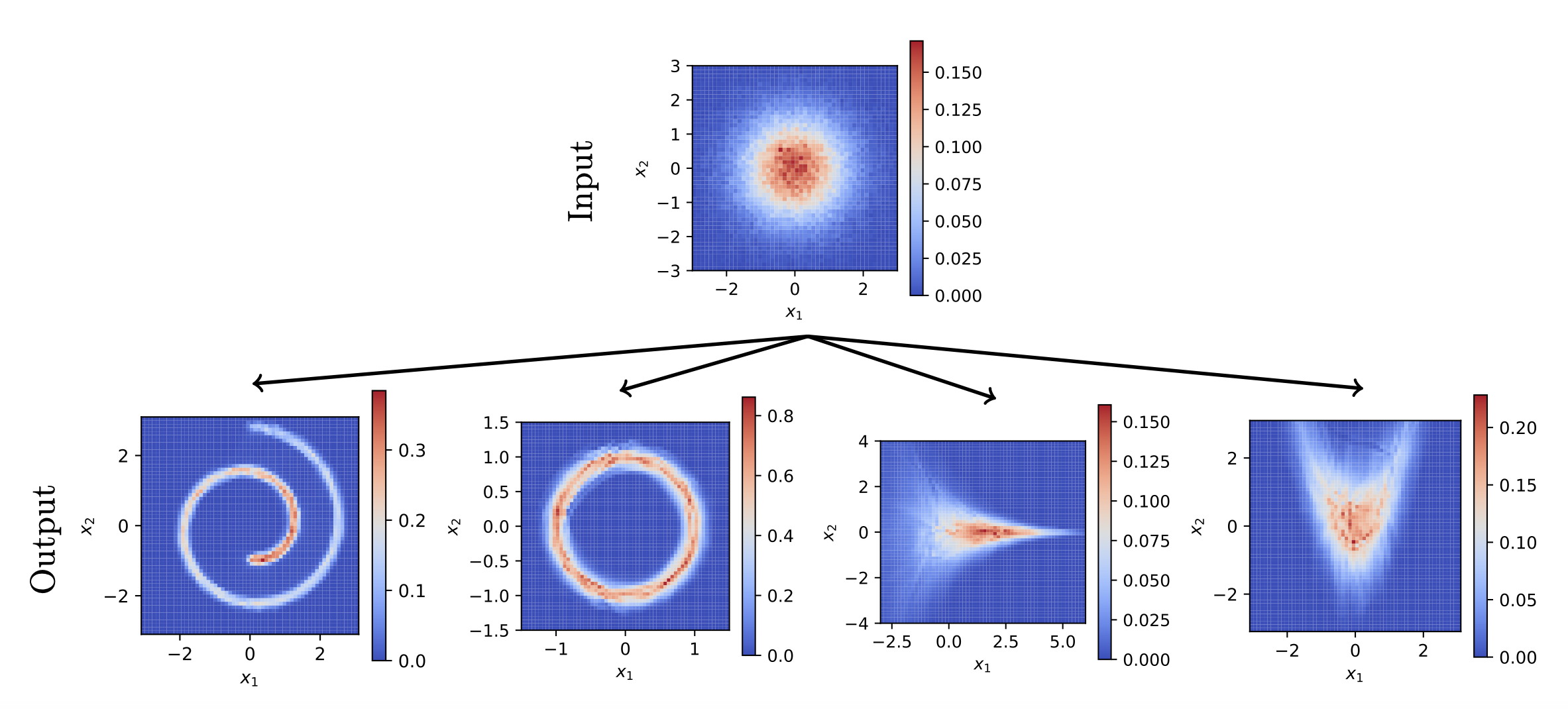
Finding the optimal map/plan between marginals is one of the most attractive problems in applied mathematics with applications in data-driven modeling and Machine Learning. I am interested in devising new dynamical systems to solve this problem more efficiently than standard methods. This includes collision-based dynamics [1], orthogonal coupling dynamics [2], and moment-based methods [3]. As a showcase, here I show the output of a generative model trained using the optimal map between the normal and four other marginals.

Visualization of optimal transport for 5 marginals

Experience

Education

Awards & Honors

Publications

Optimal Transport
Variance Reduction
Modelling in Kinetic Theory
Data-Driven Modelling
Approximating Collision Operator
Simulation of Plasma / Fluid

Presentations

Conferences

Invited Talks

Teaching

Review

I am an active referee of the following peer-reviewed journals and conferences:

Contact

You can reach me at mohsen.sadr@icloud.com